Young woman in a thoughtful pose standing in front of a blackboard that is covered in equations

Step 1: See if your integral is the correct function for this technique

For this example, we will use the following integral which has been chosen because it requires this technique. 🙂

You can check it against the formats for which this technique applies on the page with the general explanation of this technique.

Note: If you are reading this on a phone, it will work better in landscape than in portrait.

\LARGE \mathrm{\int} \normalsize \mathrm{\dfrac{1}{\sqrt{4x^2 - 9}} dx}

Step 2: Find u and du to substitute into your integral

\mathrm{Because \ it \ looks \ like \ this:} \\ \Large \mathrm{\frac{1}{\sqrt{x^2 - a^2}}}
\mathrm{We \ will \ use \ these \ substitutions:} \\ \large \mathrm{\color{blue}x = a \sec(u) \: \color{black}and \: \color{teal} dx = a \ \sec(u)\tan(u)du  \color{black} \\ for \: 0 \le u \lt \frac{\pi}{2} \ and \: \pi \le u \lt \frac{3\pi}{2}}

Step 3: Make the substitution & simplify

At this point, we will need to use the trig identities to simplify it into an easy-to-integrate form. First, we will multiple by a “fancy one” (4/4) inside the square root to force it into the x2 − a2 format so you can identify “a” easily.

\LARGE \mathrm{\int} \normalsize \mathrm{\dfrac{1}{\sqrt{4x^2 - 9}} dx =} \\ \: \\ \LARGE \mathrm{\int} \normalsize \mathrm{\dfrac{dx}{\sqrt{(\frac{4}{4})(4x^2 - 9)}} =} \\ \: \\ \LARGE \mathrm{\int} \normalsize \mathrm{\dfrac{dx}{\sqrt{4(\frac{\bcancel{4}x^2}{\bcancel{4}} - \frac{9}{4})}} =} \\ \: \\ \LARGE \mathrm{\int} \normalsize \mathrm{\dfrac{dx}{2 \sqrt{x^2 - \frac{9}{4}}} =} \\ \: \\ \dfrac{1}{2} \LARGE \mathrm{\int} \normalsize \mathrm{\dfrac{dx}{\sqrt{x^2 - \frac{9}{4}}}}
Now that this matches our standard format of \mathrm{\dfrac{1}{\sqrt{x^2 - a^2}}} , we see that: \\ \: \\ \mathrm{a = \dfrac{3}{2}} \\ \: \\

Generalizing this, you can always find “a” by dividing the constant by the coefficient of the x2 term. You can skip all of the above work as long as you remember this. I included the long way in this example so you could see where “a” comes from rather than just memorizing it without knowing why.

This means that our x and dx will be:

\\ \: \\ \boxed{ \mathrm{\color{blue} \bf x = \dfrac{3}{2}sec(u)}} \\ \: \\ and \\ \: \\ \boxed{ \mathrm{\bf \color{teal} dx = \dfrac{3}{2}\sec(u)\tan(u) \: du}} \\ \: \\
So now we substitute these expressions in place of x and dx in out integral and then simplify. Let's deal with the square root first. Note that we're starting with the original square root, not the factored one from above, but we will wind up with one-half being factored out in front of the integral just like before which is a nice double-check on our work. \\ \: \\ \mathrm{\sqrt{4x^2 - 9} =} \\ \: \\ \mathrm{\sqrt{4 \color{blue} (\dfrac{3}{2}sec(u))^2 \color{black} - 9}} \\ \: \\ \mathrm{\sqrt{4 \color{blue} (\dfrac{9}{4}sec^2(u)) \color{black} - 9}} \\ \: \\ \mathrm{\sqrt{\bcancel{4} \color{blue} (\dfrac{9}{\bcancel{4}}sec^2(u)) \color{black} - 9}} \\ \: \\ \mathrm{\sqrt{\color{blue} 9 \: sec^2(u) \color{black} - 9}} \\ \: \\ \mathrm{\sqrt{9 \: (\color{blue}sec^2(u) \color{black} - 1)}} \\ \: \\ but from our trig identities, we know that \\ \: \\ \mathrm{sec^2(u) - 1 = tan^2(u)} \\ \: \\ so our square root becomes \\ \: \\ \large \boxed{ \mathrm{\color{blue} \sqrt{4x^2 - 9} = \sqrt{9 \: \tan^2(u)} = 3 \: tan(u)}} \\ \: \\
Putting it all together, our integral becomes: \\ \: \\ \\ \: \\ \LARGE \mathrm{\int} \normalsize \mathrm{\dfrac{\color{teal} \frac{3}{2}\sec(u)\tan(u)}{\color{blue} 3 \: \tan(u)} \: \color{teal} du} \\ \: \\ \\ \: \\ \LARGE \mathrm{\int} \normalsize \mathrm{\dfrac{\bcancel{3}}{2}\dfrac{\color{teal} \sec(u)\tan(u)}{\color{blue} \bcancel{3} \: \tan(u)} \: \color{teal} du} \\ \: \\ \\ \: \\ \dfrac{1}{2} \LARGE \mathrm{\int} \normalsize \mathrm{\dfrac{\color{teal} \sec(u) \bcancel{ \tan(u)}}{\bcancel{\color{blue} \tan(u)}} \: \color{teal} du} \\ \: \\ \\ \: \\ \dfrac{1}{2} \LARGE \mathrm{\int} \normalsize \mathrm{\color{teal} \sec(u) \: du}

Step 4: Integrate

\boxed{ \dfrac{1}{2} \LARGE \mathrm{\int} \normalsize \mathrm{\sec(u) \: du = \frac{1}{2} ln|\sec(u) + \tan(u)| + C}}

Step 5: Convert back to the original variable

Substitute back to get the answer in terms of the variable that you started with.

Because we started with x = 3/2 sec(u), we need to solve for u.
First, solve for u: \\ \: \\ \large \mathrm{x = \dfrac{3}{2}\sec(u)} \\ \: \\ \large \mathrm{ \dfrac{2}{3}x = \dfrac{\bcancel{2}}{\bcancel{3}} \dfrac{\bcancel{3}}{\bcancel{2}}\sec(u)} \\ \: \\ \large \mathrm{ \sec^{-1} \left( \dfrac{2x}{3} \right) = \sec^{-1} (\sec(u))} \\ \: \\ \large \mathrm{ u = \sec^{-1} \left( \dfrac{2x}{3} \right)} \\ \: \\ We need to substitute this for u in our boxed answer above and then simplify.
\large \mathrm{\frac{1}{2} ln|\sec(u) + \tan(u)| + C} \\ \: \\ becomes \\ \: \\ \large \mathrm{\frac{1}{2} ln|\sec(\sec^{-1} \left( \frac{2x}{3} \right) + \tan(\sec^{-1} \left( \frac{2x}{3} \right))| + C} \\ \: \\ The first term isn't too bad. The secant and its inverse simply cancel each other out. \\ \: \\ \large \mathrm{\color{blue} \frac{1}{2} ln|\frac{2x}{3} + \tan(\sec^{-1} \left( \frac{2x}{3} \right))| + C \color{black}} \\ \: \\ The second term is more involved. We need to draw a triangle for this part.
A right triangle with the 90° in the lower right, and the lower left is labeled as the angle u. The adjacent side is labeled 3, the hypotenuse is 2x, and the opposite side is the square root of (2x)² - 3² which is the square root of 4x² - 9.
Because the secant is \mathrm{\frac{hypotenuse}{adjacent} = \frac{2x}{3}} , we can label the side adjacent to angle u as 3 and the hypotenuse as 2x. This means that we can use the Pythagorean Theorm to find the opposite side. \\ \: \\ \large \mathrm{a^2 + b^2 = c^2 \: so \:} \\ \: \\ \large \mathrm{b = \sqrt{c^2 - a^2}} \\ \: \\ \large \mathrm{b = \sqrt{(2x)^2 - 3^2}} \\ \: \\ \large \mathrm{b = \sqrt{4x^2 - 9}} \\ \: \\ We can now use the labeled sides to find the tangent which we know is \mathrm{\frac{opposite}{adjacent}} so our final simplification for this term is \\ \: \\ \large \mathrm{\tan(sec^{-1}(\dfrac{2x}{3})) = \dfrac{\sqrt{4x^2 - 9}}{3}} \\ \: \\ \large \mathrm{= \dfrac{\sqrt{4x^2 - 9}}{\sqrt{3^2}} = \dfrac{\sqrt{4x^2 - 9}}{\sqrt{9}}} \\ \: \\ \large \mathrm{= \sqrt{\dfrac{4x^2 - 9}{9}}} \\ \: \\ = {\large \mathrm{\color{blue} \sqrt{\dfrac{4x^2}{9} - 1}}}
Plugging this result (in blue) into the second term of our earlier blue equation, we finally get to the final answer: \\ \: \\ \boxed{ \LARGE \mathrm{\int} \normalsize \mathrm{\dfrac{1}{\sqrt{4x^2 - 9}} dx =} \large \mathrm{ \: \frac{1}{2} ln \LARGE | \normalsize \frac{2x}{3} + {\sqrt{\frac{4x^2}{9} - 1}} \LARGE | \normalsize + C \color{black}}} \\ \: \\

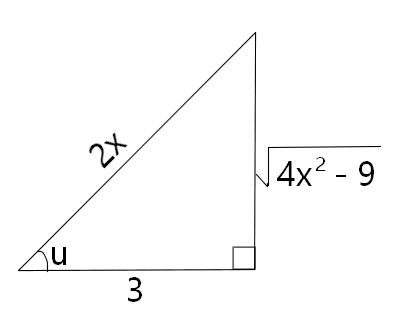
I hope this example helped. Keep practicing and it will get easier with experience.

If you have questions or thoughts about this or think of anything you would like to see covered, please leave a comment below!