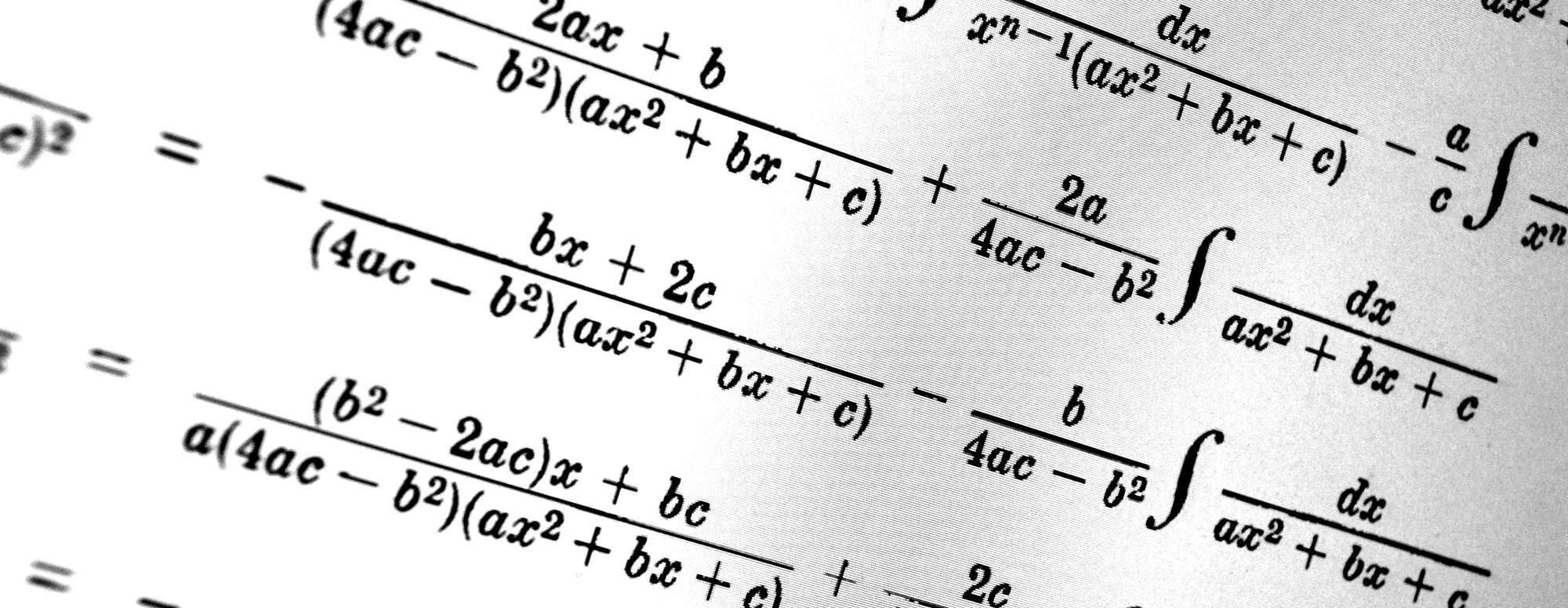
Integration techniques: Integration by Partial Fraction
Integration is the reverse of differentiation, but is quite a lot more frustrating for most people. This is the third of a series of articles on integration techniques.
Note: If you are reading this on a phone, please rotate to landscape for the longer equations so they do not run off of your screen.
Summary of Steps
Integration by Partial Fraction is used when you need to integrate a fraction that has a denominator that is a polynomial that can be factored. Basically, you break down a complicated fraction into smaller, more manageable parts, turning it into easy-to-integrate smaller parts.
I know the steps to do this look like a billion pieces right now, but after looking at examples and practicing on your own, it will become much easier. As a general overview, these are the steps:
- If necessary, divide the top by the bottom. The numerator needs to be a lower degree of of polynomial than the denominator, so if it isn’t, you have a chance to practice those dividing polynomial skills from Algebra 2 that you didn’t think you would need. 🙂
- Factor the numerator: just in case anything might cancel out with a factor from the denominator and make life a little easier.
- Factor the denominator: Take the denominator of the fraction you want to integrate and break it down into its factors.
- Express the fraction as simpler fractions: This step involves writing the original fraction as a sum of smaller fractions. Each factor becomes the denominator of its own fraction. Because we don’t yet know the numerators of the fractions, each fraction is topped with a placeholder. This part has a few rules of its own, so I will elaborate below.
- Find the unknown constants: In this step, you’ll determine the values of unknown constants from the numerators of the simpler fractions you’ve just written. I will explain this below using an example.
- Rewrite each fraction: Replace the placeholders with their values.
- Rewrite the integral: After finding the values of the constants, rewrite the original integral using the simpler fractions.
- Integrate each simpler fraction: Now, integrate each of these simpler fractions individually.
- Combine the results: Finally, put together all the integrated results from the smaller fractions to get the final answer.
I know, it feels like a lot! But it will get easier as you get the hang of it.
Expressing the fraction as smaller fractions
This part has a couple of rules to remember.
Note: For the general form, I just put a “1” on top of the fraction for simplicity because the the numerator does not affect what you will be doing with the denominator for this step.
Also, do not worry about what the A, B, and C in the numerators of the new fractions represent; we will be figuring them out in a later step.
1. For factors in the denominator that are linear, you will write fractions like this:
2. For factors in the denominator that are quadratic, you will write fractions like this:
At this point, you are probably thinking that this looks worse than what you started with, but don’t worry. It isn’t as bad as it looks!
The easiest way to see how it works is to work through some examples. I’ll work through one example on this page and add more examples later.
For this example, we will use this integral:
Step 1: If necessary, divide the top by the bottom
The numerator in this case is already a lower degree than the denominator, so we don’t need to do this step.
Step 2: Factor the Numerator
3x + 2 is already in is simplest form, so we have nothing to do for this step. It also doesn’t cancel out any terms on the bottom.
Step 3: Factor the denominator
x2 − x − 6 factors into (x − 3)(x + 2)
The roots for these factors are x = +3 and x = −2. We will use these roots in a minute, so keep them in mind.
Step 4: Express the fraction as simpler fractions
Step 5: Find the unknown constants
First, multiply through both sides with the original denominator on the left. This will clear out all of the fractions.
Remember the roots for the factors? If we plug each one in for x, we can solve for A1 and A2.
Starting with x = 3:
Now we will use x = −2 to find A2:
Step 6: Rewrite each fraction by replacing the placeholders with their values
Step 7: Rewrite the integral using the simpler fractions
Step 8: Integrate each simpler fraction
We’ll start with the first one.
And now the second integral:
Step 9: Combine the results
Put together the results of the above integrations to get your final answer.
And … just when you thought it would go on forever, you are finished!
I will be adding more examples of how to do this. If you have questions about this technique or think of anything you would like to see covered, please leave a comment below! 🙂
