The standard form:
f(x) = ax2 + bx + c
You can download a handwritten pdf of this page here: Quadratic Function Terminology
Terms & Coefficients
ax 2 – the quadratic term (It’s not a quadratic without this x2 term. 🙂 )
a is the coefficient; it includes the sign (positive or negative), but not the variable x2.
The larger the magnitude of a, the more narrow the parabola will be because the output will increase faster.
(“Magnitude” means the absolute value – ignore the sign.)
If a is:
| positive, the parabola opens upward (memory aid: positive = smile |
| negative, the parabola opens downward (memory aid: negative = frown |
(Note that the coefficient “a” is the same for both the standard and the vertex forms of the equation.)
bx – the linear term
b is the coefficient, including the sign but not the x.
If b = 0 (so there’s no linear term), the vertex and the y-intercept (vertical intercept) will be the same point.
This term moves the vertex off of the x-axis.
| If a is | and b is | the vertex will move |
| positive | positive | down & left |
| positive | negative | down & right |
| negative | positive | up & right |
| negative | negative | up & left |
c – the constant term – also known as the initial value
The constant term is what the output (y) of the equation equals when the input (x) is set equal to zero. This is why it is known as the initial value. Also, because x = 0 on the y-axis:
The vertical intercept is (0, c)
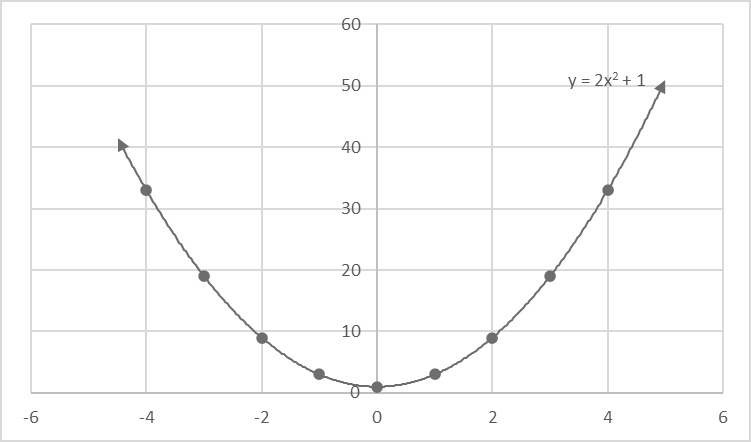
This is an example of a parabola from a quadratic equation with a positive quadratic term and no linear term. It opens upward, is symmetric around the y-axis, and the vertex is equal to the y-intercept.
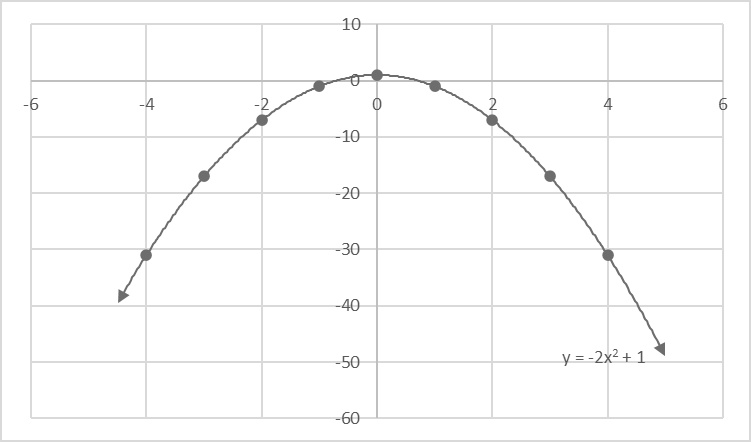
This is an example of a parabola from a quadratic equation with a negative quadratic term and no linear term. It opens downward, is symmetric around the y-axis, and the vertex is equal to the y-intercept.
Top: This is an example of a parabola from a quadratic equation with a positive quadratic term and no linear term. It opens upward, is symmetric around the y-axis, and the vertex is equal to the y-intercept.
Bottom: This is an example of a parabola from a quadratic equation with a negative quadratic term and no linear term. It opens downward, is symmetric around the y-axis, and the vertex is equal to the y-intercept.
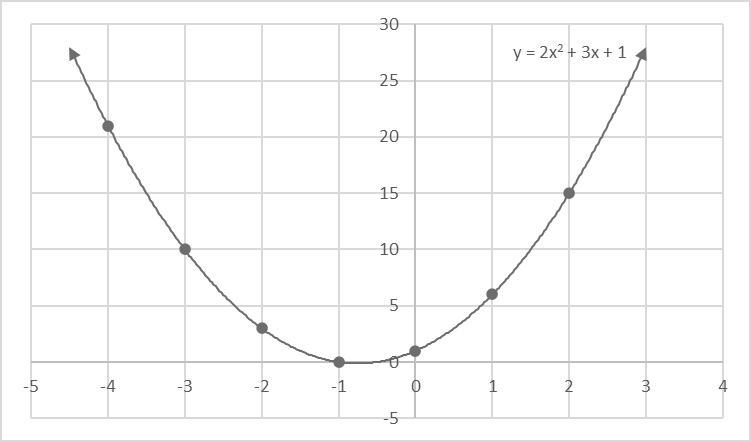
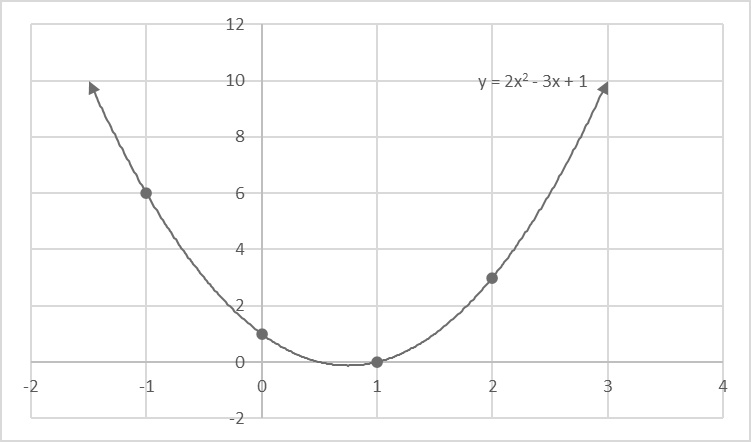
This is an example of a graph of a parabola opening upward with the vertex to the left and below the y-intercept because a and b are both positive.
This is an example of a graph of a parabola opening upward with the vertex to the right and below the y-intercept because a is positive and b is negative.
Top: This is an example of a graph of a parabola opening upward with the vertex to the left and below the y-intercept because a and b are both positive.
Bottom: This is an example of a graph of a parabola opening upward with the vertex to the right and below the y-intercept because a is positive and b is negative.
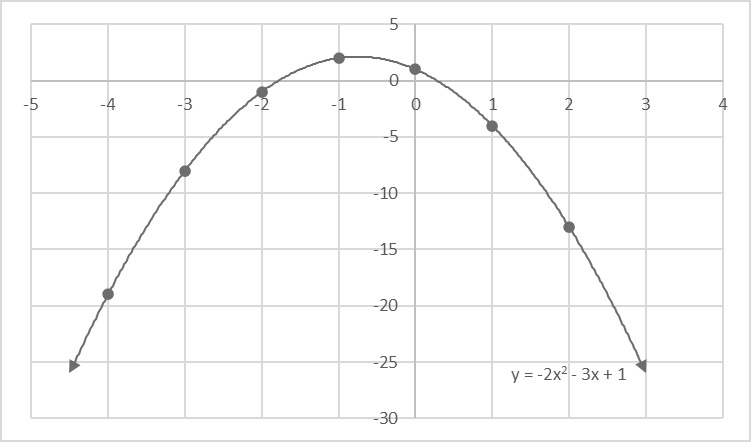
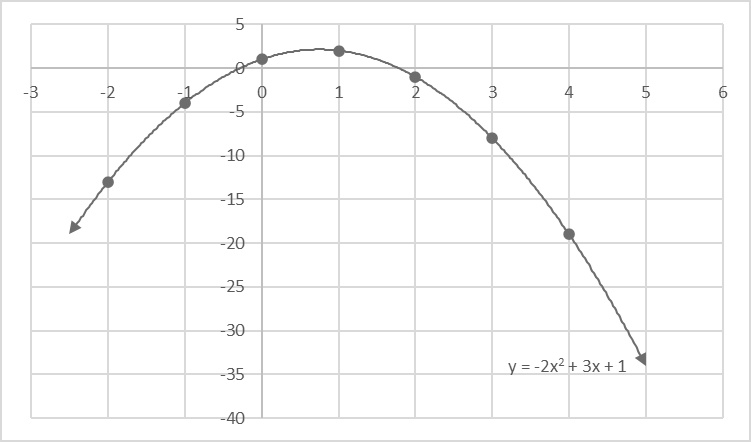
This is an example of a graph of a parabola opening upward with the vertex to the left and above the y-intercept because a and b are both negative.
This is an example of a graph of a parabola opening upward with the vertex to the right and above the y-intercept because a is negative and b is positive.
Top: This is an example of a graph of a parabola opening upward with the vertex to the left and above the y-intercept because a and b are both negative.
Bottom: This is an example of a graph of a parabola opening upward with the vertex to the right and above the y-intercept because a is negative and b is positive.
Summary of the most useful points
Most quadratic problems, especially word problems, can be answered by using 4 key points and making a quick, labeled sketch. I go over these in more detail on another page.
1. The vertical intercept, (0, c)
2. The axis of symmetry
x = −b/(2a) (The axis of symmetry is an equation and requires both sides of the equal sign.)
3. The vertex, (h, k)
h = −b/(2a) (Notice that the x-value of the vertex is the same as the value of the axis of symmetry.)
k = f(h)
4. The x-intercept(s), if any. There may be zero, one, or two x-intercepts.Find the discriminate: b2 − 4ac
If the discriminate is:
• negative, there are NO x-intercepts (no solution)
• zero, there is ONE x-intercept (one solution)
• positive, there are TWO x-intercepts (two solutions)
If the discriminate is zero or positive, solve for the x-intercepts either using the quadratic formula or by factoring. Because the discriminate is the part under the square root and you already solved that part in order to find out if there were any x-intercepts, you can just plug the single number into the square root, making the formula a bit easier to calculate.
The vertex form of a quadratic equation is covered on the “Completing the Square” page, but it looks like this:
f(x) = a(x − h)2 + k
where (h, k) is the vertex of the parabola, and a is the same as the coefficient of the quadratic term in the standard form of the equation.
Inconsistency alert: Some books call the vertex form the standard form, but I think more books label it the way I have done.
I made the graphs in Excel and then copy-pasted them into FireAlpaca to save them as jpg files.
Please let me know in the comment section below if you have any questions or ideas about what you would like to see covered, and sign up for my e-mail list for more tips and news about science and math.
